Electric potential
In Topic B.5, you learned that electric fields have a potential difference. You know need to learn about this in more detail. For this, we start electrical potential (Ve) is the energy per unit test point chrage, measured in J C-1. Just like gravitational potential, the electric potential at a distance (r) from any charge (Q) has the formula:
Ve=rkQ
However, potential varies with distance from a point charge and spherical charge:
- In a point charge: potential exponentially decreases with increasing distance from the charge.
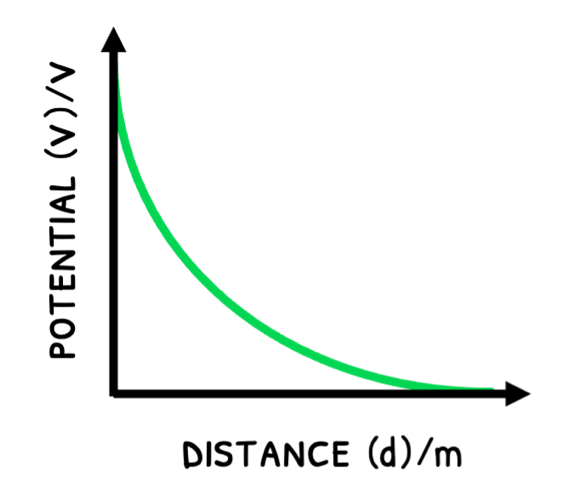
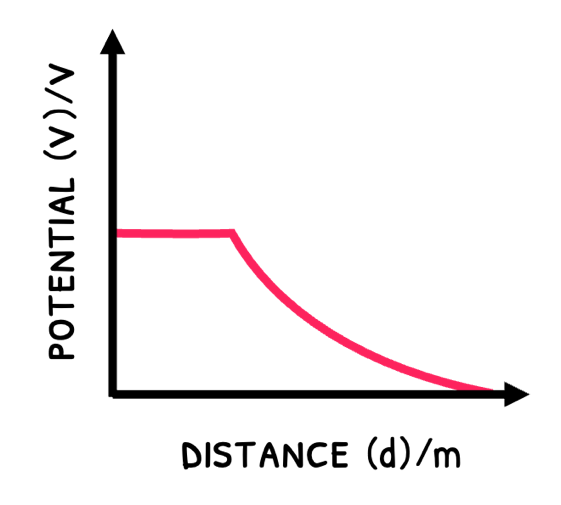
- In a spherical charge: charge is uniformly distributed so the potential is maximum until the surface. Beyond this, the potential exponentially decreases.
Remember that when a test point is moved:
- Parallel to field lines - the test point charge is moving in the direction of the force. Therefore, work is done on the object.
- Perpendicular to field lines - the test point charge is not moving in the direction of the force. Therefore, no work is done on the object.
When work is done moving a test point charge between two locations, the energy is transferred into changing its potential. Therefore, there is a electric potential difference (ΔV) between the two locations. The electric potential difference (ΔVe) is defined as the work done moving a test point charge per unit test point charge, measured in J C-1.
If work is done on the test point charge to change its potential, the potential difference will be positive. If the test point charge does work itself to change its potential, the potential difference will be negative. The formula for this is:
W=qΔVe
Equipotential
However, when no work is done in moving an object in a field, the locations must have no potential difference. These locations are said to be equipotential.
Equipotential lines are represented as lines perpendicular to the field lines, since that is the plane of motion wherein no work is done moving a test point.
For example, if the field diagram is:
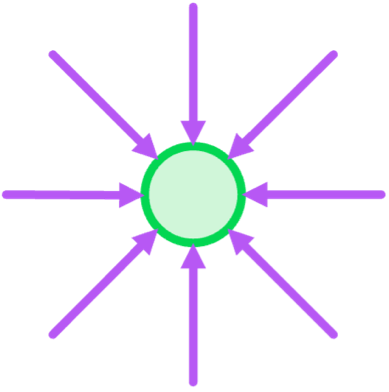
The equipotential diagram is:




