IB Chemistry Sub-topic S1.2 Notes

Mass Spectrometry 

Lastly, awkwardly nestled in this subtopic is the idea of mass spectrometry. In this subtopic, you need to understand that a mass spectrometer is a device used to:

1. Determine the fragments of a compound, covered in more detail in Topic S3.2 HL.
2. Determine an element's relative atomic mass from its isotopic composition.

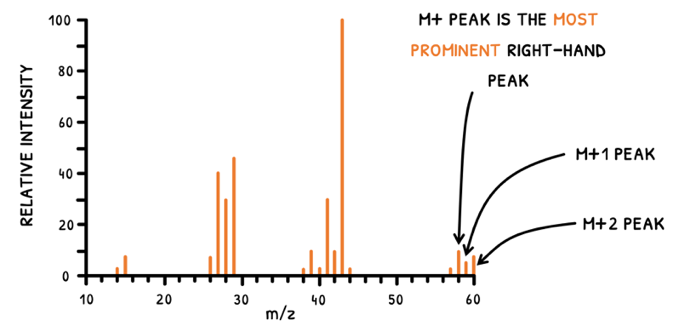
In both scenarios, the working principle is the same, but the produced information is used differently. To determine fragments, the highest peaks are used. However, you will notice that several peaks exist for each fragment, and particulary so at the M+ peak. Let's explain this:

1. An element may have two isomers with different atomic masses.
2. A mass spectrometer analyzes multiple molecules within a sample, averaging their fragment masses to produce the mass spectrum.
3. If a sample contains two isomers with:
   1. A mass difference of 1, the M+ and M+1 peaks are seen.
   2. A mass difference of 2, the M+ and M+2 peaks are seen.

There are three main isotopes to learn to easily spot these peaks:

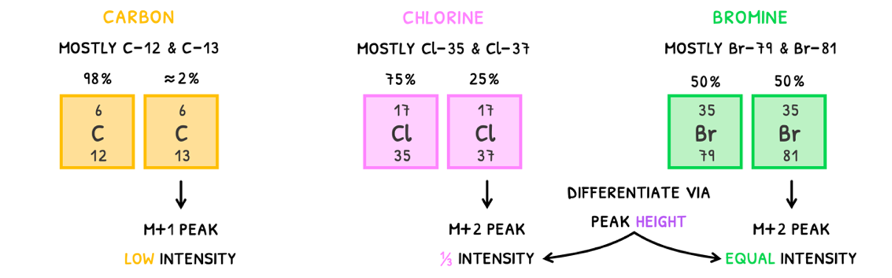
1. Carbon - mainly exists as Carbon-12 (98%) and Carbon-13 (≈2%). The Carbon-13 isomer will produce an M+1 peak but because of its low abundance, the peak will have low intensity.
2. Chlorine - mainly exists as Chlorine-35 (75%) and Chlorine-37 (25%). The Chlorine-37 isomer will produce an M+2 peak and because of its abundance, the peak will have an intensity of 33% relative to the M+ peak.
3. Bromine - mainly exists as Bromine-79 (50%) and Bromine-81 (50%). The Bromine-81 isomer will produce an M+2 peak and because of its abundance, the peak will have an intensity equal to the M+ peak.

Abundance

The resulting abundance (a) of each isotope from mass spectograms is used to then calculate an element's relative atomic mass. Although molar mass will give the exact mass for an element, relative atomic mass is the mass of an element based on the proportional natural abundance (a) of each of its isotopes. The abundance of each isotope is the ratio of its natural occurrence to the total occurrence of all isotopes.

For example, nitrogen-14 makes up 99.6% of all naturally occurring nitrogen and nitrogen-15 makes up the other 0.4% of all naturally occurring nitrogen. Therefore, nitrogen-14’s abundance is 0.996 and nitrogen-15’s abundance is 0.004.

Following on from this, if an element has three isotopes x, y, and z, its relative atomic mass is calculated by the formula:

$A_{r} = m_{x}a_{x} + m_{y}a_{y} + m_{z}a_{z}$

In trickier question, two isotopic masses (m_x and m_y) may be given, but their abundances are not given. In this scenario, used the formula:

$A_{r} = m_{x}(a_{x}) + m_{y}(1-a_{x})$

Then, plug in the relative atomic mass, the given isotopic masses and solve for x using algebra!